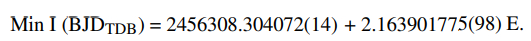This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Z. Jennings, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK (E-mail: z.jennings@keele.ac.uk);
(2) J. Southworth, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK;
(3) K. Pavlovski, Department of Physics, Faculty of Science, University of Zagreb, 10000 Zagreb, Croatia;
(4) T. Van Reeth, Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, B-3001 Leuven, Belgium.
Table of Links
- Abstract and Intro
- Observation
- Orbital Ephemeris
- Radial Velocity Analysis
- Spectral Analysis
- Analysis of the Light Curve
- Physical Properties
- Asteroseismic Analysis
- Discussion
- Conclusion, Data Availability, Acknowledgments, and References
- Appendix A: Ephemeris Determination
- Appendix B: Iteratively Prewhitened Frequencies
- Appendix C: Detected Tidally Perturbed Pulsations
3 ORBITAL EPHEMERIS

We also fitted for the linear coefficients u of the quadratic limb darkening (LD) law while quadratic terms were taken from Claret & Bloemen (2011) and Claret (2017) for the Kepler and TESS bands, respectively; we used the estimated atmospheric parameters reported in the KIC to choose the appropriate values for the quadratic coefficients. We performed fits to the WASP light curve but the lower quality of this data compared to the Kepler and TESS light curves means that including these results in the calculation of the overall preliminary eclipse model would lead to less well determined parameters. Thus, we simply include the epochs of primary minimum estimated from the WASP light curves as additional observational constraints on T0 in the preliminary fits to the Kepler and TESS light curves.
The adopted values for the light curve parameters from this preliminary analysis were taken as the weighted averages of the results from the fits to the individual Kepler quarters and TESS sectors, where the reciprocal of the squared errors from the covriance matrix were used as weights. These values are given in Table A1, and Fig. 2 shows the fit to the Kepler Quarter 0 light curve; high-frequency variability due to pulsations of the δ Scuti type is clearly visible at all orbital phases in the residuals shown in the lower panel, with amplitudes of around ±0.2 mmag.


There seems to be a trend in the O-C diagram compared with the linear ephemeris, with data points corresponding to TESS observations (>1000 cycles) all appearing above the red line. Thus, we also attempted to fit for a quadratic ephemeris, which is represented by the blue dashed line in Fig. 3. However, the corresponding quadratic term was a similar size to its errorbar. We therefore decided to stick with the linear ephemeris which was measured to be: