Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
12. Evaluation of Ξ15
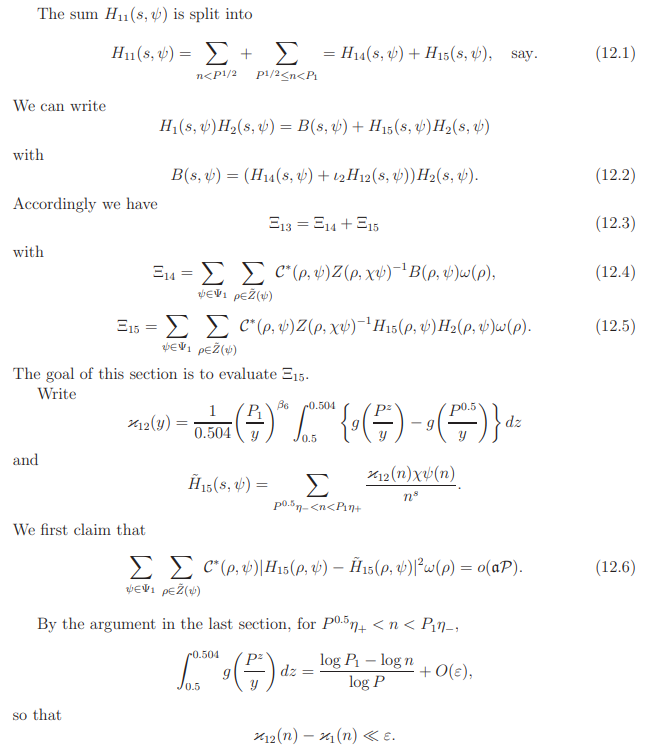
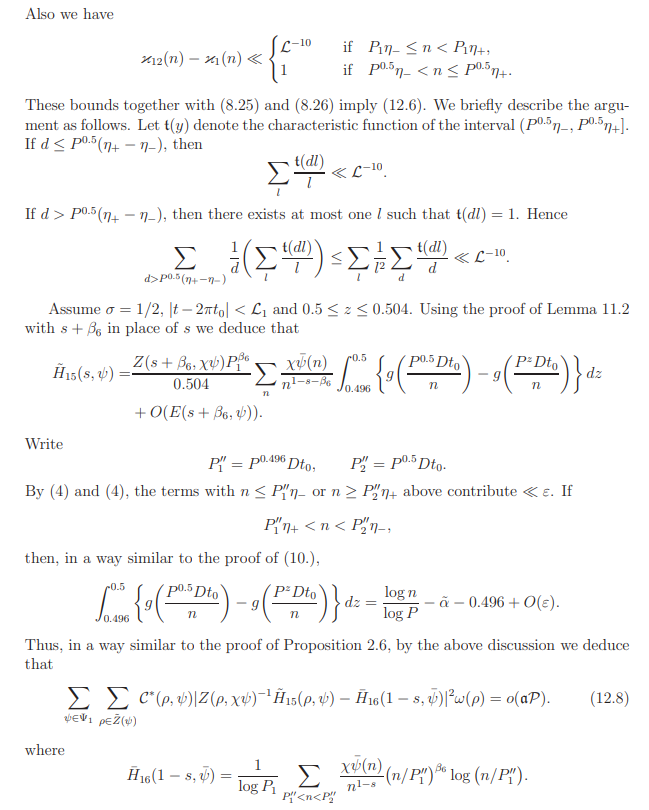


In a way similar to the proof of Lemma 8.4, by lemma 8.2 and 5.8, we find that the right side above is equal to
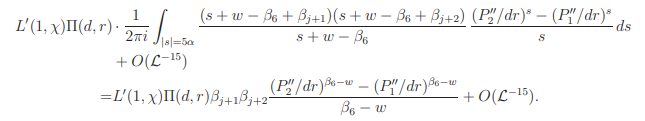
It follows by Cauchy’ integral formula that
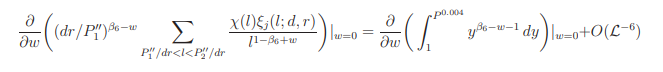
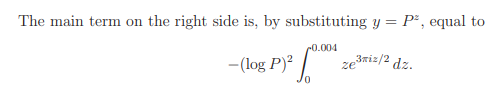
Gathering these results together we obtain (12.10). The proof of (12.11) is similar to that of.
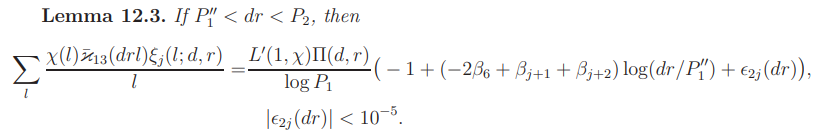
Proof. The left side is equal to
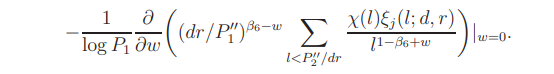
Assume |w| = α. In a way similar to the proof of Lemma 12.1, we deduce that
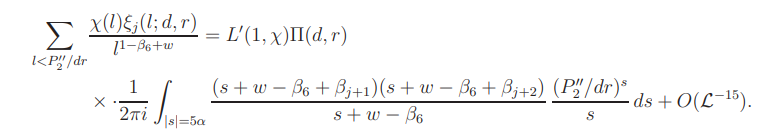
By direct calculation,
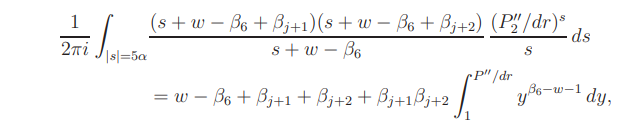
and the derivative of
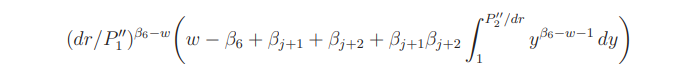
at w = 0 is equal to
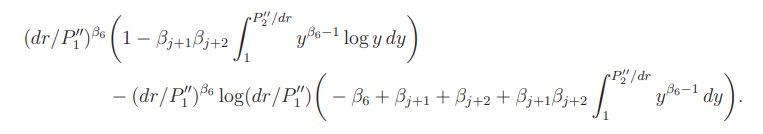
This can be written as the form

Since
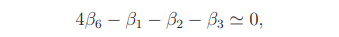
it follows by simple calculation that

We have

This paper is available on arxiv under CC 4.0 license.

