Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
Abstract
Let χ be a real primitive character to the modulus D. It is proved that
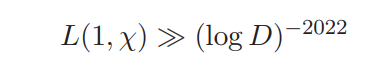
where the implied constant is absolute and effectively computable.
In the proof, the lower bound for L(1, χ) is first related to the distribution of zeros of a family of Dirichlet L-functions in a certain region, and some results on the gaps between consecutive zeros are derived. Then, by evaluating certain discrete means of the large sieve type, a contradiction can be obtained if L(1, χ) is too small.
1. Introduction

The non-vanishing of L(s, χ) near s = 1 is closely related to the lower bound for the value of L(s, χ) at s = 1. The well-known Siegel theorem [19] asserts that, for any ε > 0, there exists a positive number C1(ε) such that
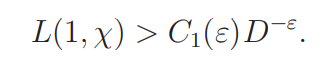
This implies, for any ε > 0, that there exists a positive number C2(ε) such that
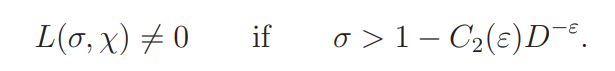

This makes the result of Siegel’s theorem entirely ineffective.
It is known (see [9]) that the non-existence of the Landau-Siegel zero implies
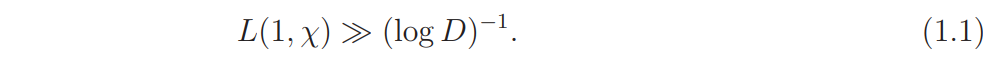
In the case χ(−1) = −1, Goldfeld [10] and Gross and Zagier [12] proved that

The main result of this paper is
Theorem 1 If χ is a real primitive character to the modulus D, then
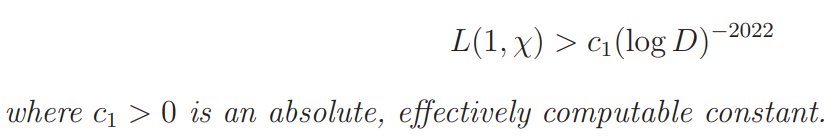
As a direct consequence of Theorem 1 we have
Theorem 2 If χ is a real primitive character to the modulus D, then
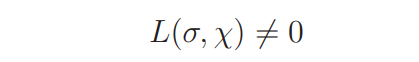
for
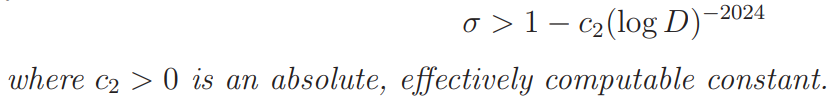
It is possible to replace the exponent −2022 in Theorem 1 by a larger (negative) value if the current arguments are modified, but we will not discuss it in this paper. On the other hand, it seems that the lower bound (1.1) can not be achieved by the present methods.
Acknowledgements. The basic ideas of the present proof were initially formed during my visit to the Institute for Advanced Study in the spring of 2014. I thank the Institute for Advanced Study for providing me with excellent conditions. I also thank Professor Peter Sarnak for his encouragement.
This paper is available on arxiv under CC 4.0 license.

