Author:
(1) Yitang Zhang.
Table of Links
- Abstract & Introduction
- Notation and outline of the proof
- The set Ψ1
- Zeros of L(s, ψ)L(s, χψ) in Ω
- Some analytic lemmas
- Approximate formula for L(s, ψ)
- Mean value formula I
- Evaluation of Ξ11
- Evaluation of Ξ12
- Proof of Proposition 2.4
- Proof of Proposition 2.6
- Evaluation of Ξ15
- Approximation to Ξ14
- Mean value formula II
- Evaluation of Φ1
- Evaluation of Φ2
- Evaluation of Φ3
- Proof of Proposition 2.5
Appendix A. Some Euler products
Appendix B. Some arithmetic sums
7. Mean-value formula I
Let N (d) denote the set of positive integers such that h ∈ N (d) if and only if every prime factor of h divides d (note that 1 ∈ N (d) for every d and N (1) = {1}). Assume 1 ≤ j ≤ 3 in what follows. Write
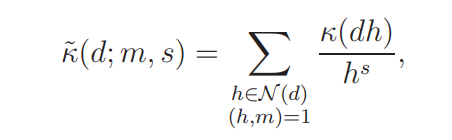
and
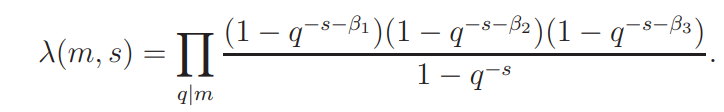
For notational simplicity we write
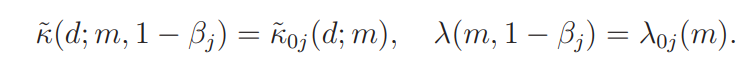
Let
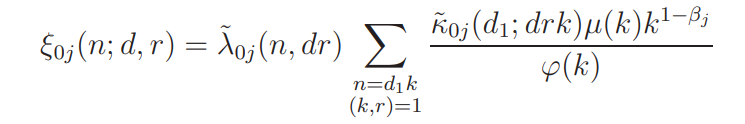
with
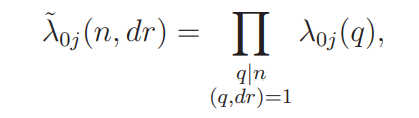
For ψ(mod p) ∈ Ψ write
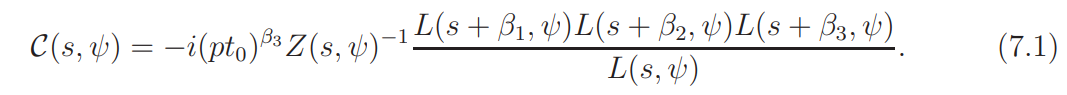
Let a = {a(n)} denote a sequence of complex numbers satisfying
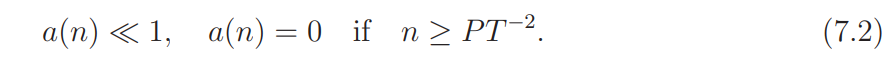
Write
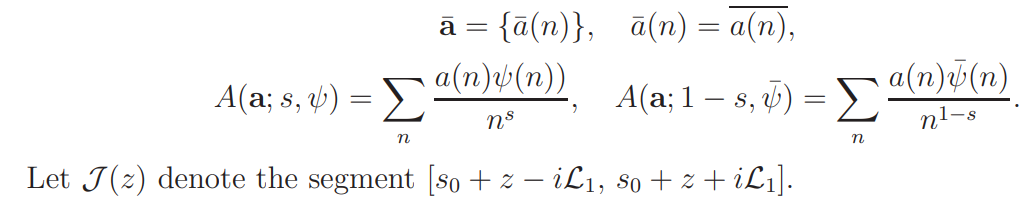
The goal of this section is to prove
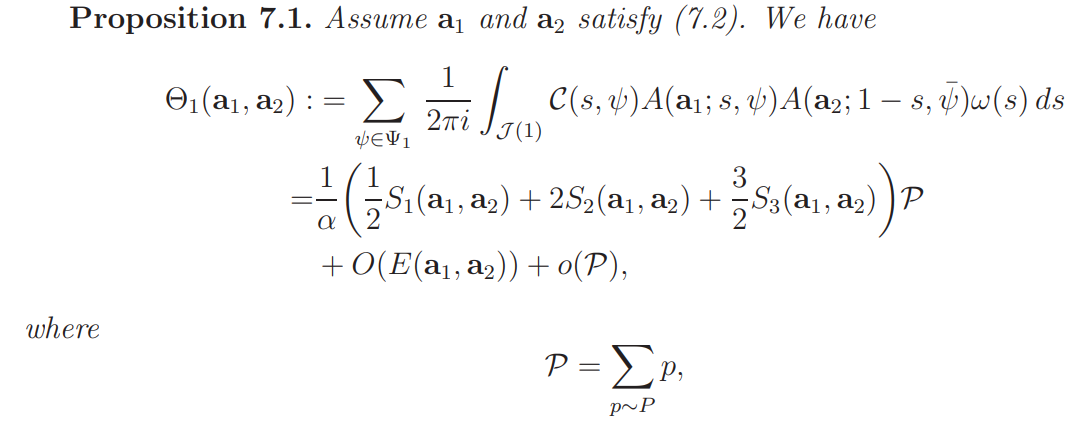
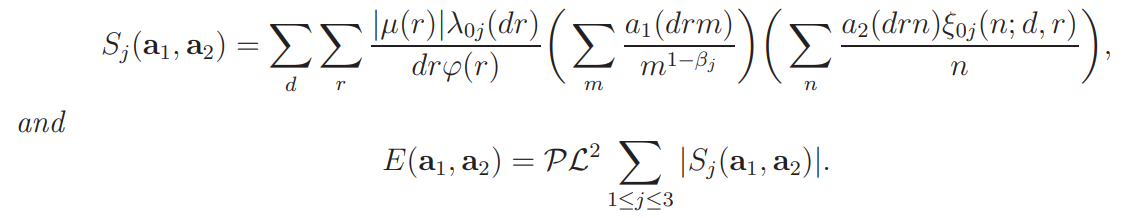
In this and the next two sections we assume that 1 ≤ j ≤ 3.
Proof of Proposition 7.1: Initial steps

Here Proposition 2.1 is crucial.
Let κ(n) be given by
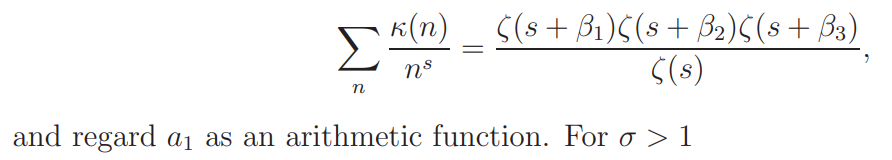
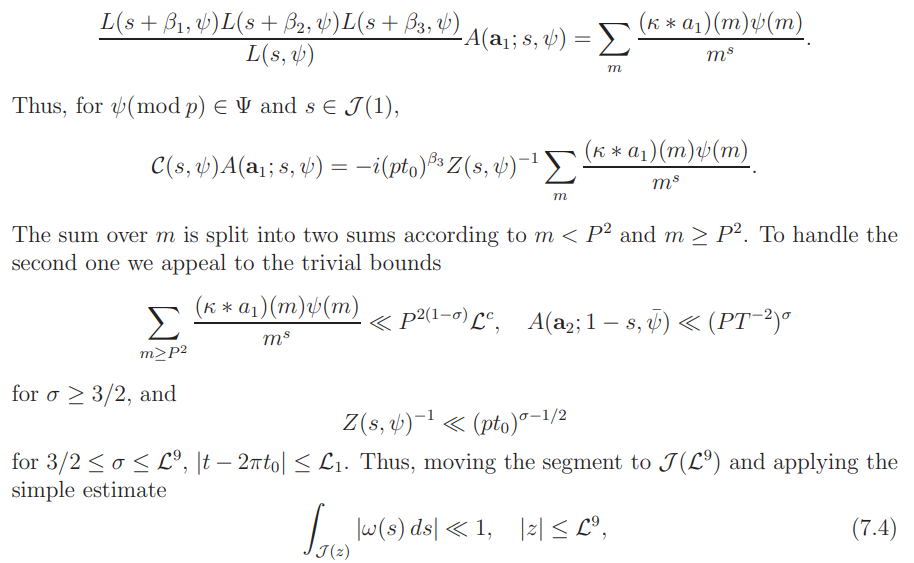
we obtain
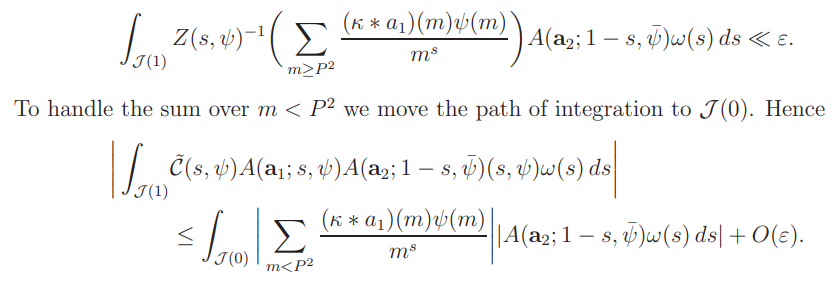
By (7.4), the proof of (7.3) is reduced to showing that
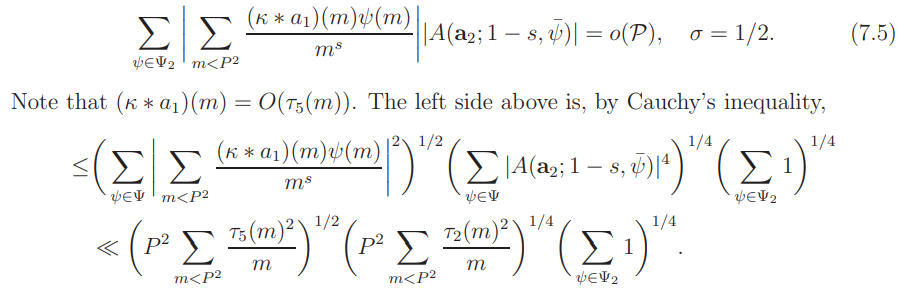
This yields (7.5) by Proposition 2.1 and (2.9).
By (7.3) we may write

This yields
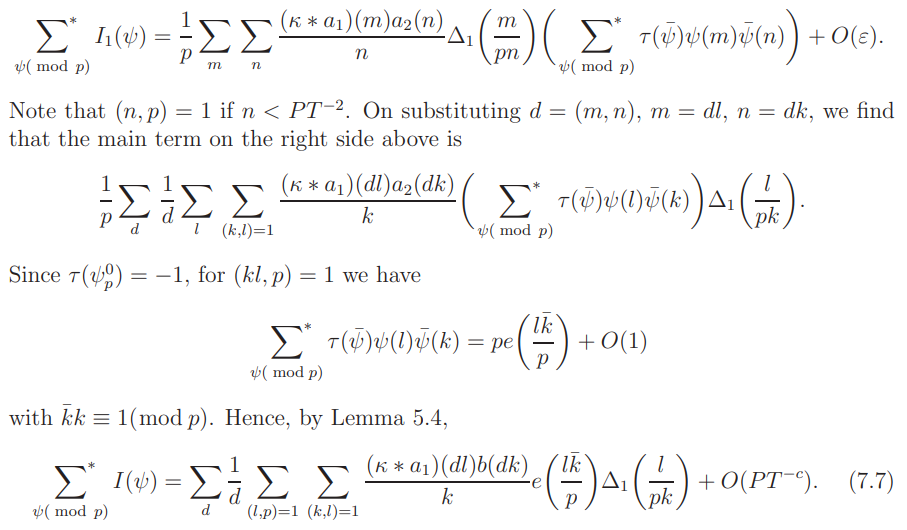
By trivial estimation, this remains valid if the constraint (l, p) = 1 is removed. Further, by the relation
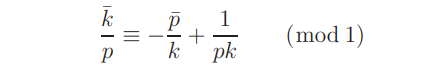
we have
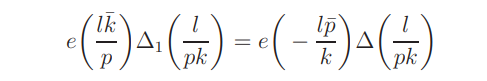
Thus the right side of (7.7) is
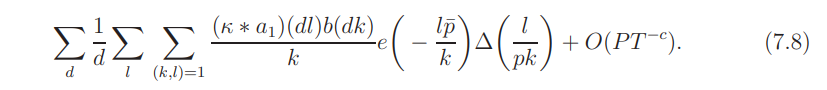
For (l, k) = 1 we have
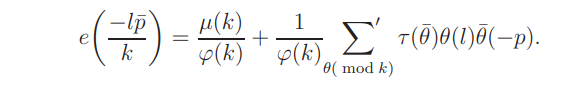
Inserting this into (7.8) we deduce that
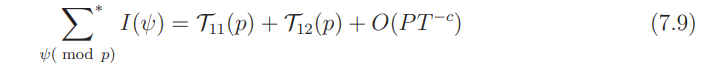
where
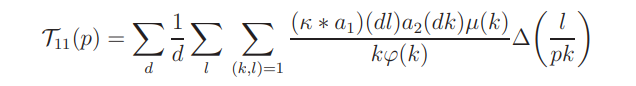
and
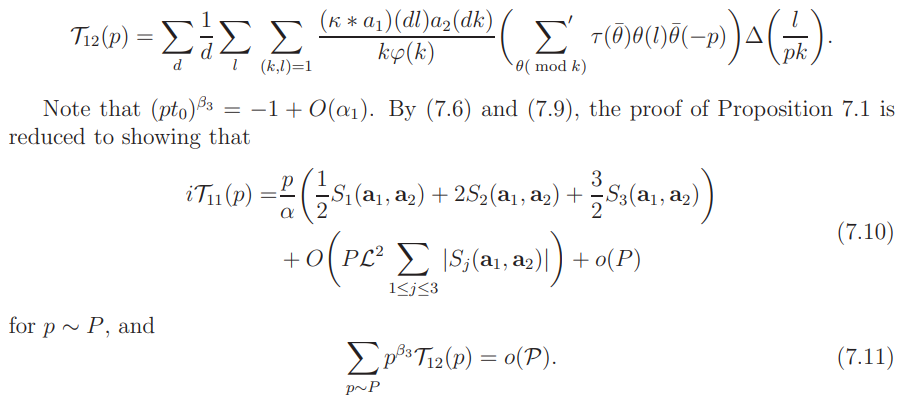
Proof of Proposition 7.1: The error term
In this subsection we prove (7.11).
Changing the order of summation gives


Assume 1 < r < D and θ is a primitive character (mod r). By Lemma 5.6, the right side of (7.14) is

which are henceforth assumed.

For σ = 1, by the large sieve inequality we have
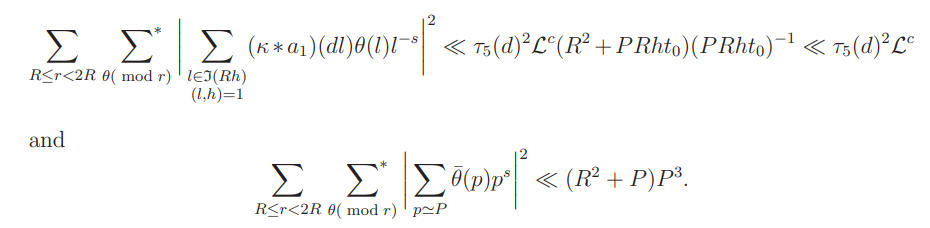
It follows by Cauchy’s inequality that
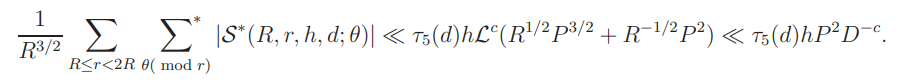
This yields (7.15).
Proof of Proposition 7.1: The main term
In this subsection we prove (7.10).
Assume p ∼ P. We may write
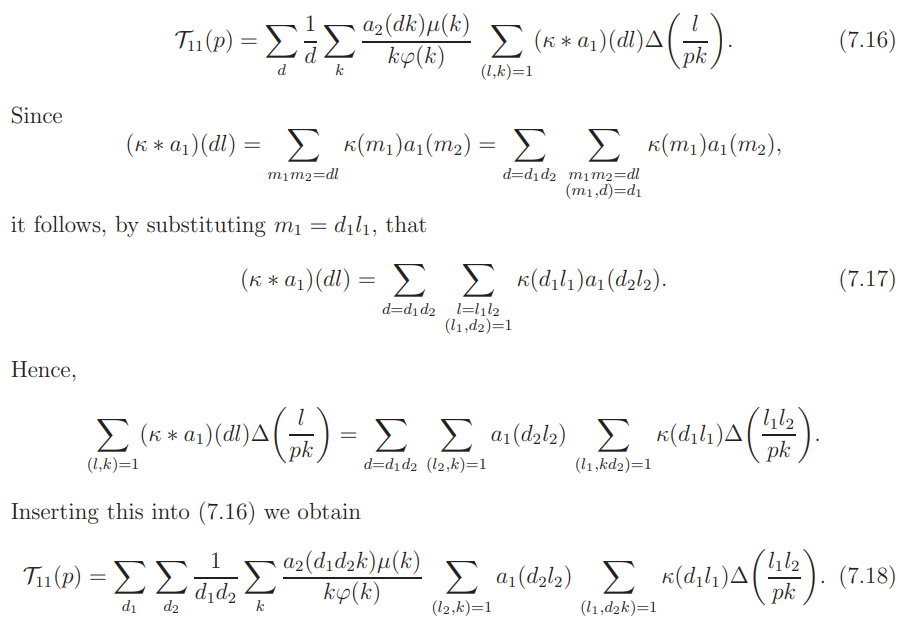
The innermost sum is, by the Mellin transform, equal to
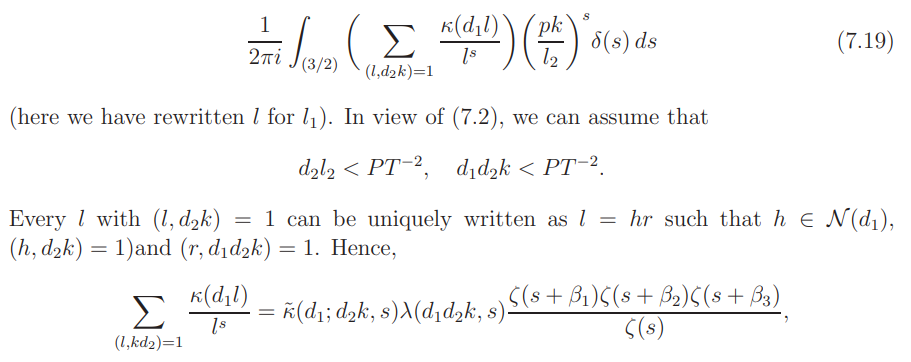
By the simple bounds
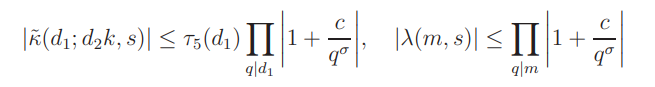
for σ > 9/10, we can move the contour of integration in (7.19) to the vertical segments
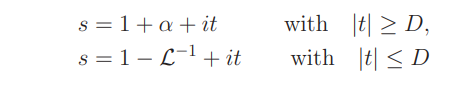
and to the two connecting horizontal segments

This yields
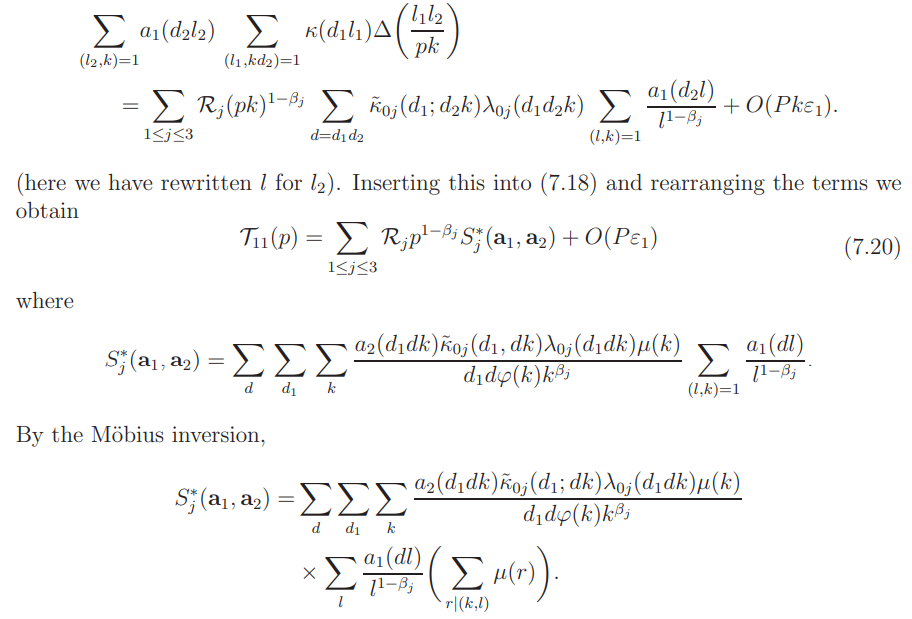
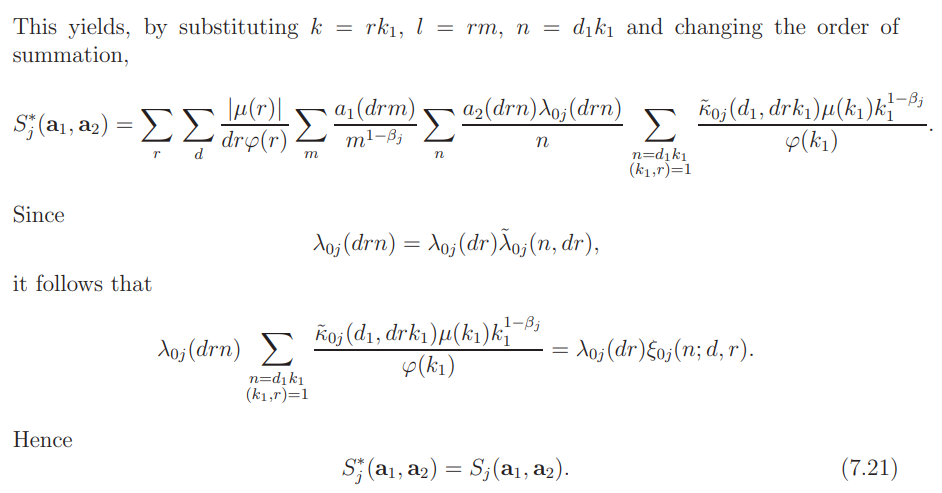
On the other hand, by Lemma 5.2 (ii) and direct calculation we have
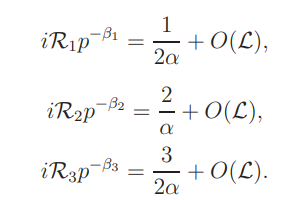
Combining these with (7.20) and (7.21) we obtain (7.10), and complete the proof of Proposition 7.1.
This paper is available on arxiv under CC 4.0 license.

