Authors:
(1) Yuxin Meng;
(2) Feng Gao;
(3) Eric Rigall;
(4) Ran Dong;
(5) Junyu Dong;
(6) Qian Du.
Table of Links
- Abstract and Intro
- Background
- Proposed Method
- Experimental Results and Analysis
- Conclusions and Future Work
- References
Abstract
Traditionally, numerical models have been deployed in oceanography studies to simulate ocean dynamics by representing physical equations. However, many factors pertaining to ocean dynamics seem to be ill-defined. We argue that transferring physical knowledge from observed data could further improve the accuracy of numerical models when predicting Sea Surface Temperature (SST). Recently, the advances in earth observation technologies have yielded a monumental growth of data. Consequently, it is imperative to explore ways in which to improve and supplement numerical models utilizing the everincreasing amounts of historical observational data. To this end, we introduce a method for SST prediction that transfers physical knowledge from historical observations to numerical models. Specifically, we use a combination of an encoder and a generative adversarial network (GAN) to capture physical knowledge from the observed data. The numerical model data is then fed into the pre-trained model to generate physics-enhanced data, which can then be used for SST prediction. Experimental results demonstrate that the proposed method considerably enhances SST prediction performance when compared to several state-of-the-art baselines.
Index Terms—Sea surface temperature, physical knowledge, generative adversarial network, numerical model
I. INTRODUCTION
N UMERICAL models have been a traditional mathematical computation method for prediction of ocean dynamics. According to the statistics from the World Climate Research Program (WCRP), the research community has developed more than 40 ocean numerical models, each of which has its own advantages and characteristics. For instance, the regional ocean model system (ROMS) [1] has a powerful ecological adjoint module, the fast ocean atmosphere model (FOAM) [2] is highly effective in global coupled ocean-atmosphere studies, the finite-volume coastal ocean model (FVCOM) [3] is capable of accurately fitting the coastline boundary and the submarine topography. The hybrid coordinate ocean model (HYCOM) [4] can implement three varieties of self-adaptive coordinates. These numerical models are not interchangeable and their use depends on the specific application. It should be noted that the various processes of ocean dynamics described in numerical models are based on simplified equations and
parameters due to our limited understanding of the ocean. The movements and changes in the real ocean are so diverse and complex that identifying the sources of a certain phenomenon becomes a real challenge. Therefore, searching for new relations or knowledge from historical data is of critical importance to improve the performance of numerical models in the study of ocean dynamics. In this paper, we refer to the capacity that can improve the numerical model as physical knowledge. We assume that the historical data may possess physical knowledge hitherto undiscovered.
Deep learning has the remarkable ability to learn highly complex functions, transforming the original data into a much higher level of abstraction. In [5], Lecun et al. described the fundamental principles and the key benefits of deep learning. Recently, deep learning has been applied to a variety of tasks, such as monitoring marine biodiversity [6], [7], target identification in sonar images [8], [9] and sea ice concentration forecasting [10]. For example, Bermant et al. [6] employed convolutional neural networks (CNNs) to classify spectrograms generated from sperm whale acoustic data. Allken et al. [7] developed a CNN model for fish species classification, leveraging synthetic data for training data augmentation. Lima et al. [8] proposed a deep transfer learning method for automatic ocean front recognition, extracting knowledge from deep CNN models trained on historical data. Xu et al. [9] presented an approach combining deep generation networks and transfer learning for sonar shipwrecks detection. Ren et al. [10] proposed an encoder–decoder framework with fully convolutional networks that can predict sea ice concentration one-week in advance with high accuracy. Through the application of deep learning-based methods to ocean research, significant improvements have been achieved in terms of classification and prediction performance.
Due to the incomplete physical knowledge in numerical models and the weak generalization performance of neural networks, there aresome efforts to improve prediction performance by combining the advantages of numerical model and nerual networks. In geographical science, this can be achieved in three different ways [11]: 1) Learning the parameters of the numerical model through neural networks. Neural networks can optimally describe the observed scene from the detailed high-resolution model, but many parameters are difficult to deduce, making their estimation challenging. Brenowitz et al. [12] trained a deep neural network based on unified physics parameterization and explained the influence of radiation and cumulus convection. 2) Replacing the numerical model with a neural network. In this way, the deep neural network architecture can capture the specified physical consistency. Pannekoucke et al. [13] translated physical equations into neural network architectures using a plug-and-play tool. 3) Analyzing the output mismatch between the numerical model and observation data. Neural networks can be used to identify, visualize, and understand the patterns of the model inaccuracies, and dynamically correct the deviation of the model. Patil et al. [14] applied the discrepancy between the results of the numerical model and the observational data to train a neural network to predict the sea surface temperature (SST). Ham et al. [15] trained a convolutional neural network based on transfer learning. They first train their model on the numerical model data, and then using reanalysis data to calibrate the model. However, the third approach has been found to suffer from a long-term bias problem, where the prediction performance deteriorates as the prediction days increase.
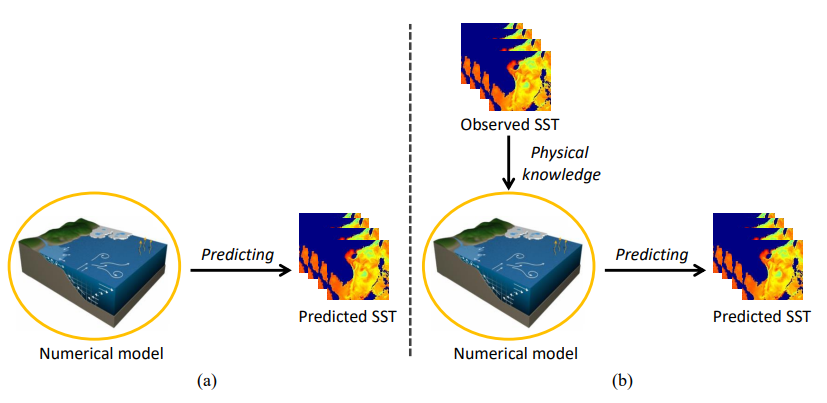
To address the above issues, in this study, we use the generative adversarial networks (GANs) to transfer the physical knowledge from the historical observed data to the numerical model data, as illustrated in Fig. 1. Different from traditional numerical model, the proposed method can correct the physical part in the numerical model data to improve the prediction performance. To be specific, as illustrated in Fig. 2, we first acquired the physical feature from the observed data by using a prior network model composed of an encoder and GAN. Thereafter, we obtained the physics-enhanced SST by feeding the numerical model data to the pretrained model. Following that, the physics-enhanced SST were adopted to train a spatial-temporal model for predicting SST. Meanwhile, we performed ablation experiments to take full advantage of the new generated data.
The main contributions of this paper are threefold:
• To the best of our knowledge, we are the first to transfer physical knowledge from the historical observed data to the numerical model data by using GANs for SST prediction.
• The difference between the enhanced data based on physical knowledge and the predicted results were exploited to adjust the weight of the model during training.
• The experimental results indicate that our proposed method can cover the shortage of physical knowledge in the numerical model and improve the prediction accuracy.
The rest of the paper is organized as follows. Section II introduces the literature review related to our method, while our method design is detailed in Section III. Then the experimental results are shown in Section IV. Section V finally concludes this paper.
This paper is available on arxiv under CC 4.0 license.

