Authors:
(1) Scott Conn, California Institute of Technology, Pasadena, California;
(2) Joseph Fitzgerald, California Institute of Technology, Pasadena, California;
(3) Jorn Callies, California Institute of Technology, Pasadena, California.
Table of Links
5. Discussion
The YBJ model does well in reproducing the mooring observations of NIWs. There are still differences between the model and the observations, however, as well as a couple of events where the YBJ model does less well. Given the observational inputs to the model, it would be surprising if this were not the case.
One major limitation is the use of altimetry for the mesoscale streamfunction. As mentioned previously, the altimetry data are a heavily smoothed version of the real field. We suggested above that some of the discrepancies between the YBJ model and the observations were due to this smoothing. We also interpolated the mesoscale vorticity onto a smaller simulation grid. The resolution of the altimetry product is 0.25◦×0.25◦ , which is larger than the size of the mooring array. Differences across the mooring array come from the interpolation between neighboring altimetry grid cells, which will have introduced interpolation errors.
Furthermore, we assumed that the mesoscale eddy field was barotropic. This is a reasonable assumption if the vertical scale of the waves is much smaller than the vertical scale of the eddies. There are certainly errors in the YBJ evolution, however, that arise from neglecting the baroclinicity of mesoscale eddies. These effects could be investigated in the future by running similar simulations using an in-situ data set that resolves the vertical structure of one or more eddies.
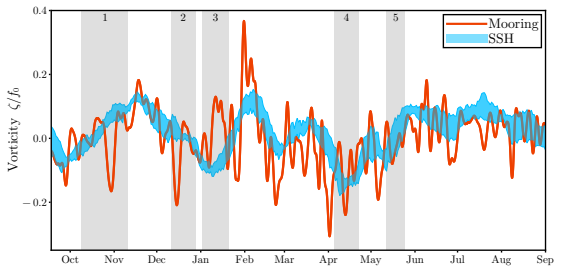
In event 1, the vorticity has large variations across the mooring array (Fig. 2a). This is reflected in the NIW observations as large differences in the amplitude across the mooring array. However, this need not be the case for all events. Event 3, by contrast, shows weak variations in the vorticity (as diagnosed from altimetry) across the mooring array.
The result is that the YBJ simulations also show weak variations in the NIW field across the mooring array region. The altimetry vorticity field is a heavily smoothed representation of the real vorticity field of the ocean; smaller scale vorticity features are invisible to measurements from altimetry. If there is little variation in the larger-scale vorticity across the mooring array, then these smaller-scale vorticity features may play a more important role in governing the variations in 𝜕𝑧𝑀.
While we do not have a spatial map of smaller-scale vorticity features, we can estimate their magnitude at the mooring array by calculating the vorticity by applying Stokes’ theorem to the area bounded by the outer moorings (Buckingham et al. 2016).
The velocity that we use in Stokes’ theorem is low-pass filtered to estimate the balanced signal. This vorticity agrees in general with the vorticity calculated from SSH but shows more high-frequency variability (Fig. 9). Event 3 shows the biggest disagreement between the two estimates of all the events. The mooring estimate shows cyclonic vorticity, whereas the altimetry estimate shows anticyclonic vorticity.
This likely explains why we see the amplitude decay much quicker in observations compared to simulations because there would have been a horizontal energy flux out of the region while the simulations have a flux into the region, which acts to maintain the amplitude. The other events show better agreement between the two vorticity estimates, although there are times where the deviation is larger. Events 1 and 2 specifically show two anticyclonic periods that are not captured by altimetry.
These may explain some of the mismatch between simulations and observations. For example, the anticyclonic excursion in event 1 probably explains why the YBJ simulation results decay more quickly than observations. For event 2, the excursion occurs primarily near the start of the event, where the NIW amplitude is weak, so its effect is tempered. Many of these anomalies are short in duration, which limits the error in using the altimetric vorticity.
The vorticity error for event 4a is minimal (Figure 9). We suspect the mismatch between the YBJ model and the observations in this event is due to the forcing. The reanalysis product used is not the exact wind-forcing felt at the OSMOSIS site. Both YBJ and PM show an initial peak in the
NIW amplitude that is not seen in the observations, indicating that the wind-stress may be wrong at this point. The forcing event seen in observations then has to destroy these waves before forcing new ones, which causes the lower amplitude of the NIW peak in the YBJ simulation compared to observations.
Notwithstanding the caveats above, it is significant that the YBJ model can reproduce much of the NIW evolution with only the mesoscale vorticity as derived from altimetry. One may expect the larger-magnitude submesoscale vorticity to be at least as important for the NIW evolution.
But the dispersion term in the YBJ equation depends on the Laplacian of 𝑀 and hence in spectral space scales as 𝜅 2 . This means that the refractive generation of small-scale structure in the wave field will be opposed by increasingly strong dispersion. Our results therefore suggest that, at the location of the mooring array, dispersion indeed outpaces refraction at submesoscales and mesoscale refraction is more important for the NIW evolution (cf., Yu et al. 2022).
Using a time-averaged stratification profile likely also contributes to differences between the observations and simulations, despite our attempts to keep simulation times as short as possible to avoid this effect. The assumption that the stratification does not vary in time is inherent in the YBJ scaling assumptions.
Related to this is the question of what depth to force the model over. We used a fixed forcing depth, although this certainly varied over the simulation periods. This problem could be side-stepped by representing the wind forcing as a surface stress and adding a parameterized turbulent vertical momentum flux to the YBJ equation to transfer momentum from the wind downwards.
The YBJ equation contains no term to represent the breaking of NIWs. The scaling 𝐻 ∗ = 𝑢 ∗ / √︁ 𝑁∗ 𝑓 , where 𝑢 ∗ = √︁ 𝜏/𝜌0 is the friction velocity and 𝑁 ∗ is the stratification at the base of the mixed layer, indicates the depth to which wind-driven turbulence could deepen the mixed layer (Pollard et al. 1973).
If the mixed layer depth is shallower than 𝐻 ∗ , the effect of NIW dissipation would be important as there is potential for mixed layer deepening by breaking of NIWs (Plueddemann and Farrar 2006). During the OSMOSIS study, Yu et al. (2022) showed that the mixed layer was generally deeper than 𝐻 ∗ .
This is especially true outside of summer and during the events we consider here. This is due to strong surface buoyancy forcing deepening the mixed layer by convection to a depth beyond what the winds alone could do. While one could include a critical Richardson number criterion to add NIW breaking to the YBJ equation, we believe that it is justifiable to ignore dissipation of NIWs in the surface layer in this study.
In event 1, the wind work predicted by YBJ agreed well with that calculated by observations. The PM model greatly overestimated the wind-work. The YBJ and PM models also disagree on the wind work for all the other events (not shown). If mesoscale interactions change the alignment of the NIWs with the winds, then this results in a very different wind work. The difference in wind work between the YBJ and PM models depends on the degree to which the mesoscale changes the alignment of the waves with the wind and the power of the winds at different frequencies.
The differences in wind work can be large for individual events but the five events we simulated are not enough to estimate what the average difference might be when averaged over many events. Nonetheless, this may provide motivation to revisit previous estimates of the NIW wind work in order to determine whether the mesoscale may modulate wind work into the NIW band globally.
This paper is available on arxiv under CC 4.0 license.

